Teoremi di Euclide e teorema di Pitagora: cosa sono e cosa definiscono

I teoremi di Euclide sono due importanti punti fermi della geometria, che hanno a che fare con il triangolo rettangolo. I due teoremi mettono in relazione le misure dei cateti, dell’ipotenusa e dell’altezza di un triangolo rettangolo con le proiezioni dei cateti sull’ipotenusa.

Euclide fu uno dei massimi esponenti nel campo della geometria piana: con i suoi teoremi, illustrati negli Elementi, ha contribuito in modo sostanziale all’evoluzione della materia e può essere considerato uno dei più brillanti matematici della Grecia antica.

Vediamo ora che cosa ci dicono questi teoremi e quali sono le caratteristiche degli enunciati.

Quello che devi sapere sui teoremi di Euclide

Quali sono le formule del triangolo rettangolo da conoscere? Che cosa significa altezza relativa all’ipotenusa? A queste (e molte altre) domande risponderemo nei prossimi paragrafi della nostra guida dedicata agli studenti dell’Università Niccolò Cusano.

LEGGI ANCHE – Teorema di Bayes: quello che devi sapere sulla probabilità condizionata

Premesse: cosa sapere prima di studiare la geometria euclidea

Per comprendere al meglio le nozioni relative ai teoremi di Euclide, dovrai avere ben chiari alcuni concetti fondamentali, senza i quali difficilmente riuscirai ad applicare correttamente questi enunciati.

Tra i prerequisiti includiamo sicuramente:

• Conoscenza del significato di congruenza ed equivalenza;
• Conoscenza e applicazione del Teorema di Pitagora;
• Saper operare con rapporti e proporzioni;
• Conoscenza del concetto di similitudine;
• Conoscenza dei criteri di similitudine dei triangoli.

Il teorema di Pitagora

Il teorema di Pitagora è un costrutto fondamentale della geometria euclidea, attribuibile al matematico Pitagora e citato anche negli Elementi di Euclide. L’enunciato afferma:

In ogni triangolo rettangolo il quadrato costruito sull’ipotenusa è equivalente all’unione dei quadrati costruiti sui cateti.

Oppure:

In ogni triangolo rettangolo l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti

Parlando della sua dimostrazione, dato un triangolo rettangolo di lati a, b e c, ed indicando con c la sua ipotenusa e con a e b i suoi cateti, il teorema si esprime con l’equazione:

a²+b² = c²

o, esplicitando c:

Le misure dei cateti sono dunque:

Primo teorema di Euclide

Abbiamo detto che i teoremi di Euclide si compongono di due enunciati. Iniziamo ora con la dimostrazione del primo teorema di Euclide.

Il primo enunciato afferma che:

In un triangolo rettangolo ogni cateto è medio proporzionale tra l’ipotenusa e la propria proiezione sull’ipotenusa.

Prendendo in esame, dunque, il triangolo rettangolo ABC, rettangolo in A, possiamo stabilire le seguenti proporzioni:

BC : AB = AB : BH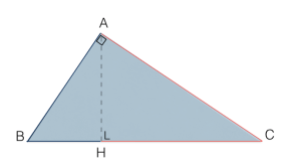

BC : AC = AC : HC

Se applichiamo le proprietà delle proporzioni, possiamo stabilire che il prodotto dei medi è uguale al prodotto degli estremi; da qui deduciamo le seguenti uguaglianze:

AB²= BC * BH

AC² = BC * CH

In sintesi, possiamo affermare che in un triangolo rettangolo il quadrato della misura di un cateto è uguale al prodotto delle misure dell’ipotenusa e della proiezione del cateto stesso sull’ipotenusa.

Secondo teorema di Euclide

Continuiamo la nostra guida illustrando il secondo teorema di Euclide, che afferma che:

In un triangolo rettangolo l’altezza relativa all’ipotenusa è media proporzionale tra le proiezioni dei due cateti sull’ipotenusa

Passiamo ora alla dimostrazione:

BH : AH = AH : HC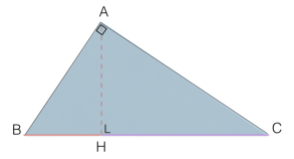

Anche in questo caso, possiamo applicare le proprietà delle proporzioni e ricavare la seguente uguaglianza:

Alla luce di questo, possiamo affermare che: in un triangolo rettangolo il quadrato della misura dell’altezza relativa all’ipotenusa è uguale al prodotto delle misure delle proiezioni dei cateti sull’ipotenusa.

Fondamenti di geometria e matematica: corsi di laurea Unicusano

Nei corsi di laurea dell’area ingegneristica dell’Università Niccolò Cusano sono presenti diversi richiami alla matematica e alla geometria. Se sei un appassionato di questa materia e desideri diventare un ingegnere, i nostri percorsi formativi sono la scelta perfetta.

I nostri corsi di laurea per diventare ingegnere sono:

• Corso di Laurea in Ingegneria Civile (triennale – classe L-7)
• Corso di Laurea Magistrale in Ingegneria Civile (biennale – classe LM-23)
• Corso di laurea Magistrale in Ingegneria Elettronica (biennale – classe LM-29)
• Corso di laurea magistrale in Ingegneria Meccanica (biennale – classe LM-33)
• Corso di laurea in Ingegneria Agroindustriale (triennale – classe L-9)
• Corso di laurea in Ingegneria Industriale Biomedica (triennale – classe L-9)
• Corso di laurea in Ingegneria Industriale Gestionale (triennale – classe L-9)
• Corso di laurea in Ingegneria Industriale Elettronica (triennale – classe L-9)
• Corso di laurea in Ingegneria Industriale Meccanica (triennale – classe L-9)

Ogni percorso formativo ha le sue peculiarità e le sue specializzazioni, da scegliere a seconda dei tuoi obiettivi e delle tue aspirazioni.

La didattica dei nostri corsi è erogata online, grazie ad una piattaforma di e-learning attiva 24 ore su 24. Il materiale didattico è costantemente aggiornato e curato dai migliori esperti del settore. La possibilità di fruire delle lezioni in ogni momento ti consente do organizzare al meglio la tua giornata e anche di coniugare studio e lavoro.

Per iscriverti ai nostri corsi di laurea, contattaci subito o chiama il numero verde 800.98.73.73